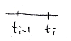Численные методы решения задачи Коши для обыкновенных дифференциальных уравнений

Найти функцию для $y(t)$ удовлетворяющую уравнению

Задача Коши для ОДУ

$\{\begin{array}{cc}{y}^{\prime }=f(t,y(t)),& t>t_0\\ y(t_0)=y_0\end{array}$

Ищем интегральную кривую, проходящую через $(t_0,y_0)$

Применяя формулу численного дифференцирования

$\frac{y(t_{i+1})-y(t_i)}{h}=f(t_i,y(t_i))\Rightarrow y_{i+1}=y_i+h\cdot f(t_i,y_i)$

Формула Тейлора

Пусть $y(t)$ - найдено. Найдем $t+h$:

$y(t+h)=y(t)+h{y}^{\prime }(t)+\frac{h^2}{2}{y}^{″}(t)+...+\frac{h^p}{p!}{y}^{(p)}(t)+\frac{h^{p+1}{y}^{(p+1)}(\xi )}{(p+1)!}$

Первая производная - это правая часть.

II-я: $y^{″}=f{\text{'}}_t+f{\text{'}}_{y}y{\text{'}}_t=f{\text{'}}_t+f{\text{'}}_{y}f$

III-я: $y^{‴}=f^{\prime }{\text{'}}_{tt}+f^{\prime }{\text{'}}_{ty}f+(f{\text{'}}_{yt}+f{\text{'}}_{yy})+f{\text{'}}_y(f{\text{'}}_t+f{\text{'}}_{y}f)$

• Формула Тейлора I-го порядка точности по $h$ (Метод Эйлера)

$y(t+h)=y(t)+hf(t,y(t))$

• Формула Тейлора II-го порядка точности по $h$:

$y(t+h)=y(t)+hf(t,y(t))+\frac{1}{2}{h}^2(f{\text{'}}_t+f{\text{'}}_{y}f)$

Метод Эйлера

$\{\begin{array}{cc}{y}^{\prime }=f(t,y(t)),& t_i=t_0+ih,i=\overline{1,n}\\ y(t_0)=y_0\end{array}$

Дискретизация задачи (переход от непрерывной функции к дискретной)

$y(t_i)$ - точное решение. $y_i$ - приближенное. $y^{\prime }(t_i)\approx h^{-1}(y_{i+1}-y_i)$, $\frac{y_{i+1}-y_i}{h}=f(t_i,y_i)$

$y^n=\left(\begin{array}{c}{y}_0\\ ⋮\\ y_N\end{array}\right)$ - в ответе получаем вектор.

$\{\begin{array}{cc}{y}_{i+1}=y_i+hf(t_i,y_i)& \\ y_0\text{ - задано}\end{array}$ шаг обычно берут h = 0.1}

Геометрическая интерпретация.

Геометрическая интерпретация метода Эйлера

$l(t)=y(t_i)+y^{\prime }(t_i)(t-t_i)$ - уравнение касательной.

Погрешности:

Модификации метода Эйлера

$y_{i+1}=y_i+h{k}_i$. изменяя $k_i$ можно легко получить меньшую погрешность.

• $k_i=f(t_{i+\frac{1}{2}},y_{i+\frac{1}{2}}$) - усовершенствованный метод Эйлера.

$\{\begin{array}{c}{y}_{i+\frac{1}{2}}=y_i+\frac{h}{2}f(t_i,y_i)\\ y_{i+1}=y_i+hf(t_{i+\frac{1}{2}},y_{i+\frac{1}{2}})\end{array}\iff y_{i+1}=y_i+h{k}_i,k_i=f(t_{i+\frac{1}{2}},y_i+\frac{h}{2}f(t_i,y_i))$ (за угол наклона берется наклон касательной в средней точке).

$E(h)=c{h}^2$

• Метод Эйлера-Коши:

$y_{i+1}+h{k}_i,k_i=\frac{k_i^1+k_i^2}{2},k_i^1=f(t_i,y_i),k_i^2=f(t_i+h,y_i+h{k}_i^2)$. $E(h)=c{h}^2$.

Методы Рунге-Кутты

Метод Эйлера - это метод Рунге-Кутты I-го порядка точности. $y_{i+1}=y_i+h{k}_i,k_i$ - угловой коэффициент секущей.

$m$-этапный метод Рунге-Кутты

$y_i=y(t_i)$

Метод Рунге-Кутты

$t_i^{(1)}=t_i$ $t_i^{(2)}=t_i^{(1)}+{\alpha }_{2}h0<{\alpha }_2<1t_i^{(m)}=t_i^{(1)}+{\alpha }_{m}h0<{\alpha }_m<1$

$k_i^{(1)}=f(t_i^{(1)},y_i^{(1)})=f(t_i,y_i)$

$k_i^{(2)}=f(t_i^{(1)}+{\alpha }_{2}h,y_i+h{\beta }_{21}{k}_i^{(1)})$

$k_i^{(3)}=f(t_i^{(1)}+{\alpha }_{3}h,y_i+h({\beta }_{31}{k}_i^{(1)}+{\beta }_{32}{k}_i^{(2)}))$

$\dots$

$k_i^{(m)}=f(t_i^{(1)}+{\alpha }_{m}h,y_i+h({\beta }_{m1}{k}_i^{(1)}+...+{\beta }_{m,m-1}{k}_i^{(m-1)}))$

Все коэффициенты ($\alpha$ и $\beta$) подлежат определению: $k_i=c_1{k}_i^{(1)}+c_2{k}_i^{(2)}+...+c_m{k}_i^{(m)}$ коэффициенты $c_i$ также неизвестны.

$y(t+h)=y(t)+h{y}^{\prime }(t)+\frac{h^2}{2}{y}^{″}(t)+...+\frac{h^p}{p!}{y}^{(p)}(t)+\overline{\stackrel{‾}{O}}(h^{p+1})$

Если хотим построить метод $p$-го порядка точности по $h$, $y_{i+1}=y_i+h{k}_i$. Возьмем разложение для точного решения. Правую часть раскладываем в $t_i$. Коэффициенты $\alpha ,\beta$ и $c$ подбираем так, чтобы разложение совпало до $p$-го порядка включительно. Построим параметрическое семейство двухэтапных методов Рунге-Кутты (2-го порядка точности по $h$)

$t_i^{(1)}=t_i,t_i^{(2)}=i_i+\alpha h$

$k_i^{(1)}=f(t_i,y_i),k_i^{(2)}=f(t_i+\alpha h,y_i+h\beta k_i^{(1)},k_i=c_1{k}_i^{(1)}+c_2{k}_i^{(2)}$

$y_{i+1}=y_i+h{k}_i=y_i+h[c_{1}f(t_i,y_i)+c_{2}f(t_i+\alpha h,y_i+h\beta k_i^{(1)})]$

$f(t_i+\alpha h,y_i+h\beta k_i^{(1)})=f(t_i,y_i)+f{\text{'}}_t(t_i,y_i)\alpha hf{\text{'}}_y(t_i,y_i)h\beta k_i^{(1)}+\overline{\stackrel{‾}{O}}(h^2)$

$y_{i+1}=y_i+h[c_{1}f(t_i,y_i)+c_2(f(t_i,y_i)+f{\text{'}}_t(t_i,y_i)\alpha h+h\beta f{\text{'}}_y(t_i,y_i)k_i^{(1)})]+\overline{\stackrel{‾}{O}}(h^3)$ - разложение приблзительного решения.

В полученное разложение будем подставлять точное решение, будем считать $\alpha =\beta$

$y^{″}(t_i)=f{\text{'}}_t(t_i,y(t_i))+f{\text{'}}_y(t-i,y(t_i))f(t_i,y_i(t_i))$

$y(t_{i+1})=y(t_i)+h(c_1+c_2)f(t_i,y(t_i))+c_2\alpha h^2[f{\text{'}}_t(t_i,y(t_i))+f{\text{'}}_y(t_i,y(t_i))f(t_i,y(t_i))]\Rightarrow y(t_{i+1})=y(t_i)+h(c_1+c_2)y^{\prime }+\alpha c_2{h}^2{y}^{″}(t_i)+\overline{\stackrel{‾}{O}}(h^3)$

$\{\begin{array}{c}{c}_1+c_2=1\\ c_2\alpha =\frac{1}{2}\end{array}\Rightarrow \{\begin{array}{c}{c}_2=\frac{1}{2\alpha }\\ c_1=1-\frac{1}{2\alpha }\end{array},\alpha$ - параметр

Имеем:

$\{\begin{array}{c}{y}_{i+1}=y_{+}h{k}_i\\ k_i^{(1)}=f(t_i,y_i)\\ k_i^{(2)}=f(t_i+\alpha h,y_i+\alpha h{k}_i^{(1)})\\ k_i=(1-\frac{1}{2\alpha })k_i^{(1)}+\frac{1}{2\alpha }{k}_i^{(2)}\end{array}$

При $\alpha =1$ получаем метод Эйлера-Коши, $\alpha =\frac{1}{2}$ - усовершенствованный метод Эйлера.

По построению: локальная погрешность этих методов для $p$-го порядка точности $l=c{h}^{p+1}$

Каноническая форма записи методов численного интегрирования

$y_{i+1}=y_i+hf(t_i,y_i)\to \frac{y_{i+1}-y_i}{h}=f(t_i,y_i)$ - явный одношаговый метод. $\frac{1}{h}\sum _{j=0}^k{\alpha }_j{y}_{i+1-j}=\mathrm{\Phi }(t_i,y_{i+1-k},...,y_i,y_{i+1},h),{\alpha }_0\ne 0$ - канонический вид формулы численного интегрирования. (неявный $k$-шаговый метод)

Если правая часть этой формулы не содержит $y_{i+1}$, тогда это явный $k$-шаговый метод. Все методы Рунге-Кутты - явные, одношаговые.

$\frac{y_{i+1}-y_i}{f}=\mathrm{\Phi }(t_i,y_i,h)$ - общая формула методов Р-К (каноническая формула явных одношаговых методов).

Шаблон:Определение Погрешность аппроксимации метода Эйлера: ${\mathrm{\Psi }}_i^h=\frac{h^2}{2}{y}^{″}(t)$

Устойчивость ЗК

$\{\begin{array}{c}{y}^{\prime }=f(t,y)\\ y(t_0)=y_0\end{array}\{\begin{array}{c}{\tilde{y}}^{\prime }=f(t,\tilde{y})-\varphi \\ \tilde{y}(t_0)={\tilde{y}}_0\end{array}$ - возмущенная задача

$\epsilon (t)=y(t)-\tilde{y}(t)\Rightarrow \{\begin{array}{c}{\epsilon }^{\prime }=f(t,y)-f(t,\tilde{y})+\varphi \\ \epsilon (t_0)=y_0-{\tilde{y}}_0={\epsilon }_0\end{array}$

$f(t,y)-f(t,\tilde{y})=f{\text{'}}_y(t,\widetilde{\stackrel{~}{y}})(y-\tilde{y})\Rightarrow \{\begin{array}{c}{\epsilon }^{\prime }=\lambda \epsilon +\varphi ,\lambda =f{\text{'}}_y(t,\widetilde{\stackrel{~}{y}}),\widetilde{\stackrel{~}{y}}=[y,\tilde{y}]\\ \epsilon (t_0)={\epsilon }_0\end{array}$

Получим линейное неоднородное уравнение

$\{\begin{array}{c}\epsilon {\text{'}}_1=\varphi \\ \epsilon (t_0)=0\end{array}$ и $\{\begin{array}{c}\epsilon {\text{'}}_2=\lambda {\epsilon }_2\\ {\epsilon }_2(t_0)={\epsilon }_0\end{array}\Rightarrow {\epsilon }_1=\underset{t_0}{\overset{t}{\int }}\varphi (\tau )d\tau ,{\epsilon }_2={\epsilon }_0\exp \{\underset{t_0}{\overset{t}{\int }}\lambda (\tau )d\tau \}$

Если $\lambda (t)>0\Rightarrow$ первое слагаемое ${\epsilon }_2\to [t\to \mathrm{\infty }]\mathrm{\infty }$. Если $\lambda (t)<0\Rightarrow {\epsilon }_2\to [t\to \mathrm{\infty }]0$

Оценка устойчивости ЗК

$|\epsilon (t)|\le k(\tau )(|{\epsilon }_0|+\underset{t_0}{\overset{\tau }{\int }}|\varphi (t)|dt),k(\tau )=\{\begin{array}{cc}\exp \{\underset{t_0}{\overset{\tau }{\int }}\lambda (t)dt\},& \lambda (t)\ge 0\\ 1,& \lambda (t)<0\end{array}$

Из этого неравенства вытекает устойчивость ЗК.

Рассмотрим возмущенную дискретную ЗК:

$\frac{1}{h}\sum _{j=0}^k{\tilde{y}}_{i+1-j}{\lambda }_j=\mathrm{\Phi }(t_i,{\tilde{y}}_{i+1-k},...,{\tilde{y}}_i,{\tilde{y}}_{i+1},h)-\varphi$

${\epsilon }_0,{\epsilon }_1,...,{\epsilon }_{k-1}$ - погрешности вычисления стартовых точек метода.

Многошаговые методы. Методы Адамса

Приближение правой части и интегрирование в многошаговых методах

$\underset{t_i}{\overset{t_{i+1}}{\int }}{y}^{\prime }dt=\underset{t_i}{\overset{t_{i+1}}{\int }}f(t,y(t))dt$. $y(t)$ приближаем полиномом по известным значениям.

Метод Адамса

Формулы Адамса-Башфорта

Метод Адамса-Башфорта

$p_1(t)=f_{i-1}+\frac{f_i-f_{i-1}}{h}(t-t_{i-1})$ - интерполяционный многочлен Ньютона. Интегрируемые функции $f(t,y)$: $\underset{t_i}{\overset{t_{i+1}}{\int }}{p}_1(t)dt=\underset{t_i}{\overset{t_{i+1}}{\int }}(f_{i-1}+\frac{f_i-f_{i-1}}{h}(t-t_{i-1}))dt=f_{i-1}h+\frac{f_i-f_{i-1}}{h}{\frac{(t-t_{i-1}{)}^2}{2}|}_{t_1}^{t_{i+1}}=\frac{h}{2}(3f_i-f_{i-1})\Rightarrow y_{i+1}=y_i+\frac{h}{2}(2f_i-f_{i-1})$ - формула А-Б (двухшаговый метод, II порядка точности по $h$) Формулы Адамаса-Мултона

Метод Адамса-Моултона

$Q_1(t)=f_i+\frac{f_{i+1}-f_i}{h}(t-t_i)$

$\underset{t_i}{\overset{t_{i+1}}{\int }}{Q}_1(t)dt=f_{i}h+{\frac{(f_{i+1}-f_i)(t-t_i{)}^2}{2h}|}_{t_1}^{t_{i+1}}=\frac{h}{2}(f_i+f_{i+1})$

$y_{i+1}=y_i+\frac{h}{2}(f_i+f_{i+1})$ - II порядка точности, более устойчив.

Порядок аппроксимации в построенных методах

${\mathrm{\Psi }}_i$ - дискретная функция. Канонический вид: $\frac{y_{i+1}-y_i}{h}=\frac{1}{2}{f}_i+\frac{1}{2}{f}_{i+1}$

$y^{\prime }=f(t,y(t))f_i=y^{\prime }(t_i)f_{i+1}=y^{\prime }(t_{i+1})$

${\mathrm{\Psi }}_i=\frac{y(t_{i+1})-y(t_i)}{h}-\frac{1}{2}{y}^{\prime }(t_i)-\frac{1}{2}{y}^{\prime }(t_{i+1})=\frac{y(t_i)+h{y}^{\prime }(t_i)\frac{h^2}{2}{y}^{″}(t_i)+\frac{h^3}{6}{y}^{‴}(t_i)+\underset{\_}{\underset{\_}{O}}(h^4)-y(t_1)}{h}-\frac{1}{2}{y}^{\prime }(t_i)-\frac{1}{2}(y^{\prime }(t_i)+h{y}^{″}(t_i)+\frac{h^2}{2}{y}^{‴}(t_i)+\underset{\_}{\underset{\_}{O}}(h^3))=\frac{h}{2}{y}^{″}(t_i)+\frac{h}{6}{y}^{‴}(t_i)+\underset{\_}{\underset{\_}{O}}(h^3)-\frac{h}{2}{y}^{″}(t_i)-\frac{h^2}{4}{y}^{‴}(t_i)+\underset{\_}{\underset{\_}{O}}(h^3)=-\frac{h^2}{12}{y}^{‴}(t_i)+\underset{\_}{\underset{\_}{O}}(h^3)$

${\mathrm{\Psi }}_i=-\frac{h^2}{12}{y}^{‴}(t_i),\mathrm{\Psi }=\max 0\le i\le N|{\mathrm{\Psi }}_i|\le \frac{M_3{h}^2}{12}\Rightarrow$ II аппроксимационный порядок

Если функция $y(t)$ - аналитична и $k$ раз дифференцируема, то $k$ - шаговый метод А-Б и $k-1$ шаговый метод А-М имеют $k$-й порядок аппроксимации по $h$.

Каноническая формула метода:

$(A):\frac{1}{h}\sum _{j=0}^k{\alpha }_j{y}_{i+1-j}=\mathrm{\Phi }(t_i,y_{i+1-k},...,y_i,y_{i+1})$ - дискретная ЗК. Стартовые точки $y_0,y_1,...,y_{k-1}$

$(B):\frac{1}{h}\sum _{j=0}^k{\alpha }_j{y}_{i+1-j}^{*}=\mathrm{\Phi }(t_i,y_{i+1-k}^{*},...,y_i^{*},y_{i+1}^{*})$ - дискретная ЗК с возмущенными данными. Стартовые точки $y_0,y_1,...,y_{k-1}$

Уравнения высокого порядка и системы ДУ

$\{\begin{array}{c}y{\text{'}}_1=f_1(t,y,...,y_m)\\ y{\text{'}}_2=f_2(t,y,...,y_m)\\ ⋮\\ y{\text{'}}_m=f_m(t,y,...,y_m)\\ y{\text{'}}_1(t_0)=y_1^0\\ ⋮\\ y{\text{'}}_m(t_0)=y_m^0\end{array}$ - нелинейная система ОДУ 1-го

$y=\left(\begin{array}{c}{y}_1\\ ⋮\\ y_m\end{array}\right)y^0=\left(\begin{array}{c}{y}_1^0\\ ⋮\\ y_m^0\end{array}\right)F=\left(\begin{array}{c}{f}_1(t,y_1,...,t_m)\\ ⋮\\ f_1(t,y_1,...,t_m)\end{array}\right)$

метод Эйлера:

$\{\begin{array}{c}{y}^{\prime }=F(t,y)\\ y(t_0)=y_0\end{array}$

$y_{i+1}=y_i+hF(t_i,y_i)$

$\{\begin{array}{c}{a}_m{y}^{(m)}(t)+a_{m-1}{y}^{(m-1)}+...+a_1{y}^{\prime }(t)+a_{0}y(t)=f(t)\\ y(t_0)=y_0\\ ⋮\\ y^{(m-1)}(t_0)=y_0^{(m-1)}\end{array}$

$y_1(t)=y(t);y_2(t)=y^{\prime }(t)=;...;y_m(t)=y^{(m-1)}(t)$ - замены

$\{\begin{array}{c}y{\text{'}}_1=y_2\\ y{\text{'}}_2=y_3\\ ⋮\\ y{\text{'}}_{m-1}=y_m\\ y{\text{'}}_m=\frac{f(t)-a_{m-1}{y}_m-...-a_0{y}_1}{a_m}\end{array}y=\left(\begin{array}{c}{y}_1\\ ⋮\\ y_m\end{array}\right)F=\left(\begin{array}{c}{y}_2\\ ⋮\\ y_m\\ \frac{f(t)-a_{m-1}{y}_m-...-a_0{y}_1}{a_m}\end{array}\right)$

Устойчивость численных методов

$\frac{1}{h}\sum _{j=0}^k{\alpha }_j{y}_{n+1-j}=\mathrm{\Phi }(t_n,y_{n+1-k},...,y_n,y_{n+1},h)(1)$

${\alpha }_0,{\alpha }_1,...,{\alpha }_{k-1}{\alpha }_0\ne 0$

Чтобы облегчить задачу будем исследовать устойчивость по начальным данным (без правой части) $y_0,y_1,...,y_{k-1}$

Рассмотрим модельную задачу $y^{\prime }=0$ на нуль-устойчивость

$\frac{1}{h}\sum _{j=0}^k{\alpha }_j{y}_{n+1-j}=0$

$(2){\alpha }_0{y}_{n+1}+{\alpha }_1{y}_n+...+y_k{\alpha }_{n+1-k}=0$ - конечно-разностное уравнение. Стартовые точки $y_{n+1-k}...y_{n+1}$

Затем мы находим $y_0,y_1,...,y_{k-1},y_k,y_{k+1},...,y_N$

Возмущенная задача: $y_0^{*}...y_{k-1}^{*}$

${\alpha }_0{y}_{n+1}^{*}+{\alpha }_1{y}_n^{*}+...+{\alpha }_k{y}_{n+1-k}^{*}=0$

$y_i^{*}i=\overline{0,N}$ - проверим на устойчивость

${\alpha }_0{\epsilon }_{n+1}+{\alpha }_1{\epsilon }_n+...+{\alpha }_k{\epsilon }_{n+1-k}=0$

${\epsilon }_n=\bar{\epsilon }{q}^n$, $q$ некоторое число. $\bar{\epsilon }$ - некоторая первоначальная погрешность. Получим характеристическое уравнения $k$ - шагового метода:

${\alpha }_0{q}^k+{\alpha }_1{q}^{k-1}+...+{\alpha }_k=0$

$P(q)=\sum _{j=0}^k{\alpha }_k{q}^{k-j}$ - характеристический полном Уравнение $P(q)=0$ имеет ровно $k$ корней (кратных и простых). Пусть $q_1$ - кратный корень кратности $r$, остальные простые:

$q=c_1^{(1)}{q}_1^n+c_1^{(2)}n{q}^n+...+c_1^{(r-1)}{n}^{r-1}{q}_1^n+c_2{q}_2^n+...+c_m{q}_m^n(3)$

Общее решение уравнения: $|q_i|<1,n\to \mathrm{\infty },|q|\to 0$

Шаблон:Утверждение Р-К: $P(q)=q-1$

А: ${\alpha }_0{q}^k+{\alpha }_1{q}^{k-1}+0q^{k-2}+...+0=0{\alpha }_0=1,{\alpha }_1=-1P(q)=q^k-q^{k-1}$

Наличие $O$-устойчивости означает, что метод устойчив на конечном отрезке $[t_0,T]$. Если $T\to \mathrm{\infty }$ следует применять абсолютно устойчивые методы.

Модельная задача:

$\{\begin{array}{cc}{y}^{\prime }=\lambda y& \lambda \in C\\ y(t_0)=y_0& Re\lambda <0\end{array}\}\Rightarrow$ Ассимптотическая устойчивость

$\frac{1}{h}\sum _{j=0}^k{\alpha }_j{y}_{n+1-j}=\lambda \sum _{j=0}^k{\beta }_j(\lambda h)y_{n+1-j}z=\lambda h$

$\sum _{j=0}^k({\alpha }_j-z{\beta }_j(z))y_{n+1-j}=0\gamma ={\alpha }_j-z{\beta }_j(z)$

Для невозмущенной задачи: $\sum _{j=0}^k{\gamma }_j{y}_{n+1-j}=0y_0,...,y_{k-1}$ - стартовые точки

$P(q,z)={\gamma }_0{q}^k+{\gamma }_1{q}^{k-1}+...+{\gamma }_k=0$. Ищем $q_1,q_2,...,q_n$ (зависят от $z$)

Для явного метода Эйлера: $\frac{y_{n+1}-y_n}{h}=\lambda y_n$

${\epsilon }_{n+1}-(1+\lambda h){\epsilon }_n=0q-(1+z)=0\Rightarrow q_1=1+z|1+z|<1$

$-1<1+z<1\Rightarrow z\in (-2,0)z=\lambda h;\lambda <0\Rightarrow 0<h<\frac{2}{-\lambda }$

Метод называется устойчивым при ограничении на шаг $h<\frac{2}{|\lambda |}$

Для неявного:

$\frac{y_{n+1}-y_n}{h}=\lambda y_{n+1}\Rightarrow \frac{1}{1-\lambda h}=q\Rightarrow |1-\lambda h|<1$ - верно т.к. $\lambda <0$

Ограничений на $h$ нет. Область устойчивости: $|1-z|<1$

Неявный метод Эйлера $A$-устойчив

Понятие о жестких задачах

$S=\frac{\max |Re{\lambda }_i(A)|}{\min |Re{\lambda }_i(A)|},S$ - число жесткости системы

$s\gg 10$ - система жесткая. Для таких задач надо применять $A$-жесткие методы.